Binary Search Tree In java

Binary search tree is a node based binary tree data structure which has following property:

1. The left subtree of a node contains key that is less than the node's key.

2. The right subtree of a node contains key that is greater than the node's key.

3. The left and right subtree must also be binary search tree.

Create a node to store the key

class Node
{
	int data;
	Node left;
	Node right;
	public Node(int data)
	{
	    this.data = data;
	    this.left = null;
	    this.right = null;
	}
}

Create a class BST

class BST
{
	Node root;
	static int count = 0;
	public BST()
	{
		root = null;
	}
}

Add method is used to add the key in binary search tree.

void add(int key)
{ 
       root = addHelper(root, key); 
}

Node addHelper(Node root, int key) { 
     if (root == null) { 
        root = new Node(key); 
        return root; 
       } 
      if (key < root.data) 
          root.left = addHelper(root.left, key); 
      else if (key > root.data) 
           root.right = addHelper(root.right, key); 
        return root; 
 } 

Delete a particular key in a binary search tree.

public Node deleteNode(Node root, int key)
{
      Node parent = null;
      Node curr = root;

      while (curr != null && curr.data != key)
      {
	   parent = curr;
	   if (key < curr.data) {
		curr = curr.left;
	    }
	    else {
		   curr = curr.right;
	     }
	}

	 // return if key is not found in the tree
	if (curr == null) {
		return root;
	}

		// node to be deleted has no children i.e. it is a leaf node
	if (curr.left == null && curr.right == null)
	{
	      // if node to be deleted is not a root node, then set its
	      // parent left/right child to null
	      if (curr != root) {
			if (parent.left == curr) {
				parent.left = null;
			} else {
				parent.right = null;
			}
		}
		// if tree has only root node, delete it and set root to null
		else {
			root = null;
		}
	}

		// node to be deleted has two children
	else if (curr.left != null && curr.right != null)
	{
		// find its in-order successor node
		Node successor  = minimumKey(curr.right);
		int val = successor.data;
		deleteNode(root, successor.data);
		curr.data = val;
	}

		// node to be deleted has only one child
	else
	{
		// find child node
		Node child = (curr.left != null)? curr.left: curr.right;

		// if node to be deleted is not a root node, then set its parent
		// to its child
		if (curr != root)
		{
			if (curr == parent.left) {
				parent.left = child;
			} else {
				parent.right = child;
			}
		}

		// if node to be deleted is root node, then set the root to child
		else {
			root = child;
		}
	}
	       return root;
}

Finding the minimum value from binary search tree.

public Node minimumKey(Node curr)
{
	while (curr.left != null) {
		curr = curr.left;
	}
	return curr;
}

Searching a node of given key in binary search tree.

public Node search(Node root,int key)
{
	if(root == null) {
		return null;
	}

	if(root.data == key) {
		return root;
	}
	else if(key<root.data) {
		return search(root.left,key);
	}
	else {
		return search(root.right,key);
	}
}

Kth Smallest in binary search tree.

public static Node kthSmallest(Node root, int k) 
{ 
       if (root == null) 
           return null; 
  
        Node left = kthSmallest(root.left, k); 
       
        if (left != null) 
            return left; 
      
        count++; 
        if (count == k) 
            return root; 
     
        return kthSmallest(root.right, k); 
    } 
    
    
    public static void printKthSmallest(Node root, int k) 
    { 
        count = 0;
        Node curr = kthSmallest(root, k); 
        if (curr == null) 
            System.out.print("There are less "
                        + "than k nodes in the BST"); 
        else
            System.out.print(curr.data); 
    } 

Inorder in binary search tree.

 public void inOrder(Node root)
 {
    	if(root == null) {
    		return;
    	}

    	inOrder(root.left);
    	System.out.print(root.data+" ");
    	inOrder(root.right);
  }

Preorder in binary search tree.

    public void preOrder(Node root)
    {
    	if(root == null) {
    		return;
    	}

    	System.out.print(root.data+" ");
    	preOrder(root.left);
    	preOrder(root.right);
    }

Postorder in binary search tree.

public void postOrder(Node root)
    {
    	if(root == null) {
    		return;
    	}

    	postOrder(root.left);
    	postOrder(root.right);
    	System.out.print(root.data+" ");
    }

Driver method.

public static void main(String[] args)
    {
    	BST tree = new BST(); 
    	tree.add(5); 
        tree.add(3); 
        tree.add(2); 
        tree.add(4); 
        tree.add(7); 
        tree.add(6); 
        tree.add(8);


        System.out.println("Inorder of BST *********************************");
        tree.inOrder(tree.root);
        System.out.println();
        System.out.println("Preorder of BST *********************************");
        tree.preOrder(tree.root);
        System.out.println();
        System.out.println("Postorder of BST *********************************");
        tree.postOrder(tree.root);
        System.out.println();
        System.out.println("Delete 4 from BST*********************************");
        int key = 4;
        tree.root = tree.deleteNode(tree.root,key);
        System.out.println("Inorder of BST *********************************");
        tree.inOrder(tree.root);
        System.out.println();
         System.out.println("Delete 7 from BST*********************************");
        key = 7;
        tree.root = tree.deleteNode(tree.root,key);
        System.out.println("Inorder of BST *********************************");
        tree.inOrder(tree.root);
        System.out.println();
        System.out.println("Minimum key from BST ****************************");
        Node curr = tree.minimumKey(tree.root);
        System.out.print(curr.data);
        System.out.println();
        System.out.println("Search a node from BST ****************************");
        key = 2;
        curr = tree.search(tree.root,key);
        System.out.print(curr.data+" ");
        System.out.println();
        System.out.println("Kth smallest in BST ****************************");
        int k = 3;
        tree.printKthSmallest(tree.root,k);
        System.out.println();
    }

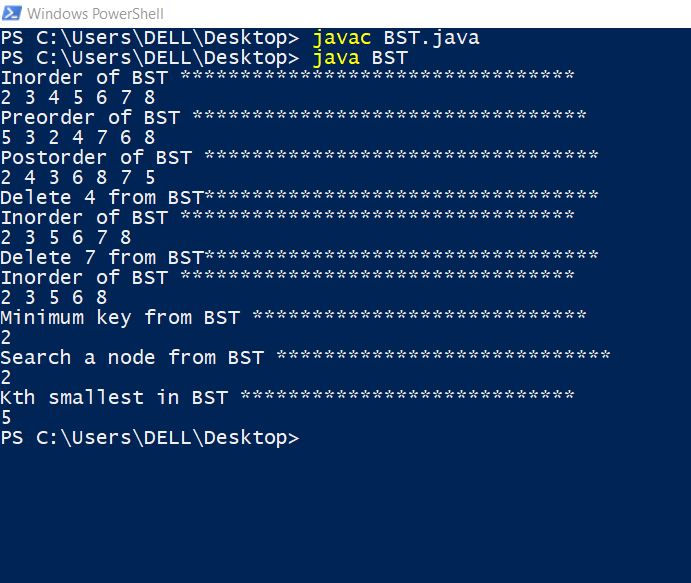
Output