Lexical Text Similarity (NLP)
- Pratibha

- Jan 14, 2022
- 3 min read

To calculate similarity between two documents/text is one of the most common task in NLP and yet it is the most active topic of research as well. In this blog we will discuss how to measure lexical similarity between text and the math behind it.
What is Text Similarity?
Determining the closeness of two pieces of text or document in terms of surface meaning or implied meaning is called text similarity.
There are two ways to measure text similarity:
1. Lexical similarity: If the similarity is decided based on the surface meaning.
Example:
a. Her face lit up.
b. Her candle lit up itself.
The two sentences a and b are mostly composed of same set of words: 'Her', 'lit' and 'up'. This makes them lexically similar. Although the meaning conveyed by them is very different.
2. Semantic similarity: If the similarity is decided based on the implied meaning.
Example:
a. It is Gandhi's biography .
b. This books talks about the life of Gandhi.
The two sentences a and b are not composed of similar words but they convey the same meaning.
Measuring Lexical Similarity
Vector representation:

In order to work with text data using a machine we first need to transform it into a form which is easily understood by the machine. We do this by converting the sentences into vectors. There are different ways to get it done. If you are not familiar with the concept please check out this blog.
Let us consider the following sentences:
a. Her face lit up.
b. Her candle lit up itself.
c. Candle was lighted.
Vector of sentence a: [1, 1, 1, 1, 0, 0, 0, 0]
Vector of sentence b: [1, 0, 1, 1, 1, 1, 0, 0]
Vector of sentence c: [0, 0, 0, 0, 1, 0, 1, 1]
It should be noted that these vectors are a simple representation of absence or presence of words in a sentence out of set of all the unique words from both sentences. Thus, it only represents lexicality and does not account for implied meaning (semantic meaning) in any way.
Now that the sentences have been converted into vectors. We can simply use mathematics to find the measure of closeness between the two vectors.
The closer the vectors in vector space, the more lexically similar the vectors.
We can measure the closeness of vectors by either calculating the distance between them or by calculating the angle between them.
We can use the following metrics to measure the closeness of vectors in terms of distance of angle:
Euclidean distance
Cosine similarity
Jaccard similarity
Euclidean distance:
To calculate Euclidean distance we use the following formula:
Given vectors:
A = [1, 1, 1, 1, 0, 0, 0, 0]
B = [1, 0, 1, 1, 1, 1, 0, 0]
C = [0, 0, 0, 0, 1, 0, 1, 1]
d(A, B) = ((1-1)^2 + (1-0)^2 + (1-1)^2 + (1-1)^2 + (0-1)^2 + (0-1)^2 + 0 + 0)^1/2
d(A, B) = 1.732
d(A, C) = ((0-1)^2 + (0-1)^2 + (0-1)^2 + (0-1)^2 + (1-0)^2 + 0 + (1-0)^2 + (1-0)^2)^1/2
d(A, C) = 2.645
Based on our results we can see that sentence B is more lexically similar to sentence A as compared to sentence C. Although sentence B and C talk about similar thing.
We can use Euclidean distance to measure the similarity but it is not a popular practice because this method is biased by size difference in vector representations.
To avoid such issue, instead of calculating the distance between the vectors we can calculate the angle between them.
Cosine similarity:
To avoid the issue of bias in case of Euclidean distance, instead of calculating the distance between the vectors we can calculate the cosine of the angle between them using the following formula:

Given vectors:
A = [1, 1, 1, 1, 0, 0, 0, 0]
B = [1, 0, 1, 1, 1, 1, 0, 0]
C = [0, 0, 0, 0, 1, 0, 1, 1]
cos(A, B) = 0.6708
cos(A, C) = 0.0
It should be noted that cosine value ranges from 0 to 1 where 0 represents no match and 1 represents strong match.
Jaccard Similarity:
In the above two approach we had to convert the sentences into their vector representation. In case of Jaccard similarity we don't need to convert the sentences into vector.
Jaccard similarity can be calculated as:
size of common words in the two sentences / size of unique words in the two sentences.
Thus,
J(A,B) = (no. of common words in A and B)/ (no. of unique words in A + no. of unique words in B)
J(A, B) = 3/(1+2) = 1
J(A, C) = 0/(4+3) = 0
The higher the value of Jaccard similarity the higher the similarity of the text.
In the methods we have covered so far if we have to choose the best one, then the winner will be cosine similarity. But based on use case any of these method can be chosen to produce better results.
You may also be interest in the following blogs:
If you need implementation for any of the topics mentioned above or assignment help on any of its variants, feel free contact us.

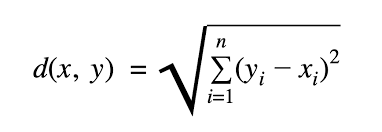



Comments