Need help with Singular Value Decomposition (SVD) Assignment Help or Singular Value Decomposition (SVD) Project Help? At Codersarts we offer session with expert, Code mentorship, Code mentorship, Course Training, and ongoing development projects. Get help from vetted Machine Learning engineers, mentors, experts, and tutors.
Are you stuck with your assignment? Are you looking for help in Singular Value Decomposition (SVD) Assignment Help? Are you looking for an expert who can help in your assignment? We have an expert team of Data science professionals who would be available to work on Singular Value Decomposition (SVD) Assignment. Our team will understand the requirements and will complete the assignment flawlessly and plagiarism free. Our expert will assure you that you will provide the best solutions for your assignment. Our Singular Value Decomposition (SVD) Assignment helps experts write the assignment according to the requirement given by the professor and by thoroughly following the university guidelines. Our expert will help you secure higher grades in the examination. We will complete the assignment before the time span with the best solution. Our Singular Value Decomposition (SVD) Assignment help expert will provide the proper guidance and complete solution for your assignment.
What is Singular Value Decomposition (SVD) ?
In linear algebra, the singular value decomposition (SVD) is a factorization of a real or complex matrix. It generalizes the eigendecomposition of a square normal matrix with an orthonormal eigenbasis to any {\displaystyle m\times n}m\times n matrix. It is related to polar decomposition.
Let A be an m × n matrix. The Singular Value Decomposition (SVD) of A,
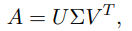
where U is m × m and orthogonal, V is n × n and orthogonal, and Σ is an m × n diagonal matrix with nonnegative diagonal entries
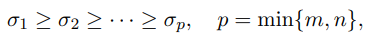
known as the singular values of A, is an extremely useful decomposition that yields much information about A, including its range, null space, rank, and 2-norm condition number. We now discuss a practical algorithm for computing the SVD of A, due to Golub and Kahan.
Let U and V have column partitions
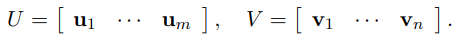
From the relations
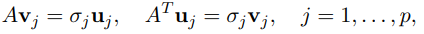
it follows that
That is, the squares of the singular values are the eigenvalues of AT A, which is a symmetric matrix.
It follows that one approach to computing the SVD of A is to apply the symmetric QR algorithm to AT A to obtain a decomposition AT A = V Σ T ΣV T . Then, the relations Avj = σjuj , j = 1, . . . , p, can be used in conjunction with the QR factorization with column pivoting to obtain U. However, this approach is not the most practical, because of the expense and loss of information incurred from computing AT A.
Instead, we can implicitly apply the symmetric QR algorithm to AT A. As the first step of the symmetric QR algorithm is to use Householder reflections to reduce the matrix to tridiagonal form, we can use Householder reflections to instead reduce A to upper bidiagonal form
It follows that T = BT B is symmetric and tridiagonal. We could then apply the symmetric QR algorithm directly to T, but, again, to avoid the loss of information from computing T explicitly, we implicitly apply the QR algorithm to T by performing the following steps during each iteration:
How Codersarts can Help you in Singular Value Decomposition (SVD) Algorithm Assignment?
Codersarts provide:
Singular Value Decomposition (SVD) Assignment help
Singular Value Decomposition (SVD) or Singular Value Decomposition (SVD) Project Help
Mentorship in Singular Value Decomposition (SVD) from Experts
Singular Value Decomposition (SVD) Development Project
If you are looking for any kind of Help in Singular Value Decomposition (SVD) Assignment or Singular Value Decomposition (SVD) Project Contact us
Comments